Dynamische Elektrische Felder

Elektrodynamik - Das zeitliche Verhalten einer räumlich ausgedehnten Raumladungsdichte im homogenen, linearen, isotropen Medium

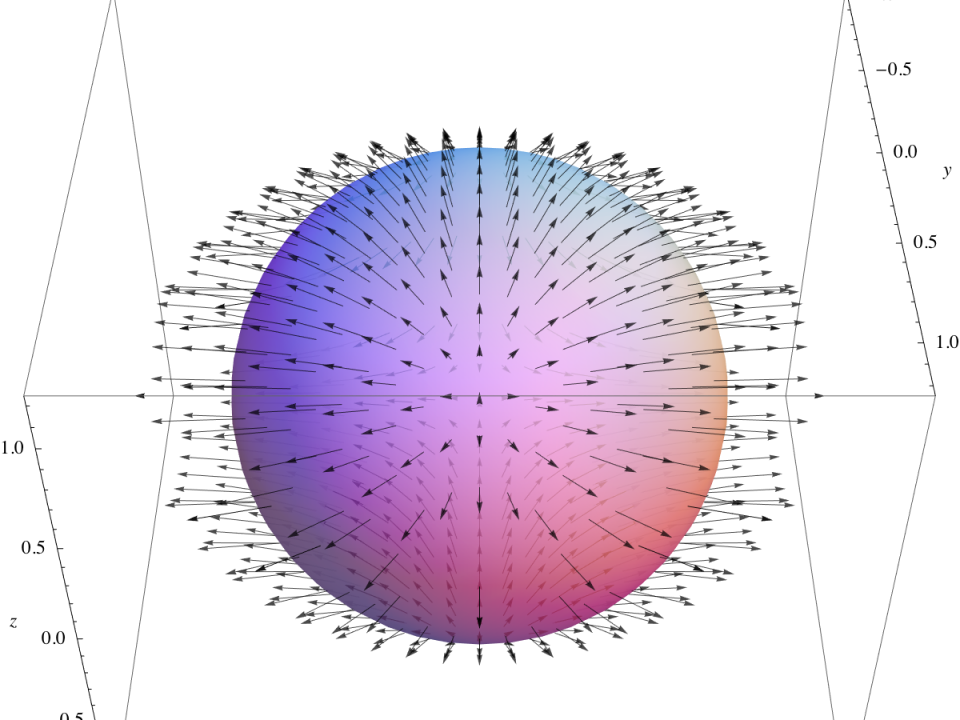
Gegeben sei eine kugelförmig mit dem Radius​​ R​​ ausgedehnte Raumladungsdichte​​ ρ0​​ zur Zeit t = 0 im unendlich ausgedehnten Material (dielektrische Konstante​​ ε, magnetische peamiabilität​​ μ​​ und Leitfähigkeit​​ κ). Diffusionseffekte werden vernachlässigt.​​ Nun wird untersucht wie sich die ​​ elektrodynamische Umgebung ab dem Zeitpunkt t = 0 verhält?

Es gilt nach dem Durchflutungsgesetz (4. Maxwellgleichung):

∇×H⃑=J⃑+∂∂tD⃑

Entsprechend gilt bei Anwendung der Divergenz:

​​ 

0=∇∙∇×H⃑=∇J⃑+∇∂∂tD⃑

Nach dem Gausschen Gesetz für elektrische Felder (1. Maxwellsche Gleichung) gilt:

∇D⃑=ρ

Aus der Linearität der Ableitung folgt mit obiger Formel:

0=∇J⃑+∂∂tρ

Gleichzeitig gilt mit​​ J⃑=κεD⃑

∇J⃑=∇κεD⃑=κε∇D⃑=κερ

Nach einsetzen in obere Gleichung ergibt sich folgende lineare homogene gewöhnliche Differentialgleichung ersten Gerades:

0=κερ+∂∂tρ

Laplacetransformiert also:

κεΡs+sΡs-ρt=0=0

Ρs=ρt=0κε+s

Die Lösung der DGL ist nach der inversen Laplacetransformation:

ρ=ρt=0e- κεt=ρ0e- κεt

Das elektrische Feld entwickelt sich nach der ersten Maxwellgleichung zu:

∭Vρ0e- κεt dV=∯AD⃑dA⃑

Aufgrund der Kugelsymmetrie gilt in Kugelkoordinaten​​ D⃑=Drrer⃑​​ und folglich:

∭Vρ0e- κεt dV=43πr3ρ0e- κεt   für r<R43πR3ρ0e- κεt   für R≤r=∫02π∫0πDrrr2sin⁡φ dφ dϑ

43πr3ρ0e- κεt   für r<R43πR3ρ0e- κεt   für R≤r=4πDrrr2

Nach​​ Drr​​ umgestellt ergibt sich für​​ D⃑:

D⃑=13rρ0e- κεt er⃑   für r<R13R3r2ρ0e- κεt er⃑   für R≤r

Nun gilt:​​ E⃑=1εD⃑

Energetische Betrachtung:

Offensichtlich​​ ist zum Zeitpunkt t=0 Energie ausschließlich im elektrischen Feld gespeichert. Dies ist dadurch begründet, dass ein radiales Feld kein quellenfreies Feld sein kann, ein eventuelles Magnetfeld jedoch geometrisch bedingt zwingend ein radiales Feld sein muss. Auf Grund der Quellenfreiheit des Magnetfeldes nach der zweiten Maxwellschen Gleichung​​ ∇B⃑=0​​ muss gelten​​ B⃑=0