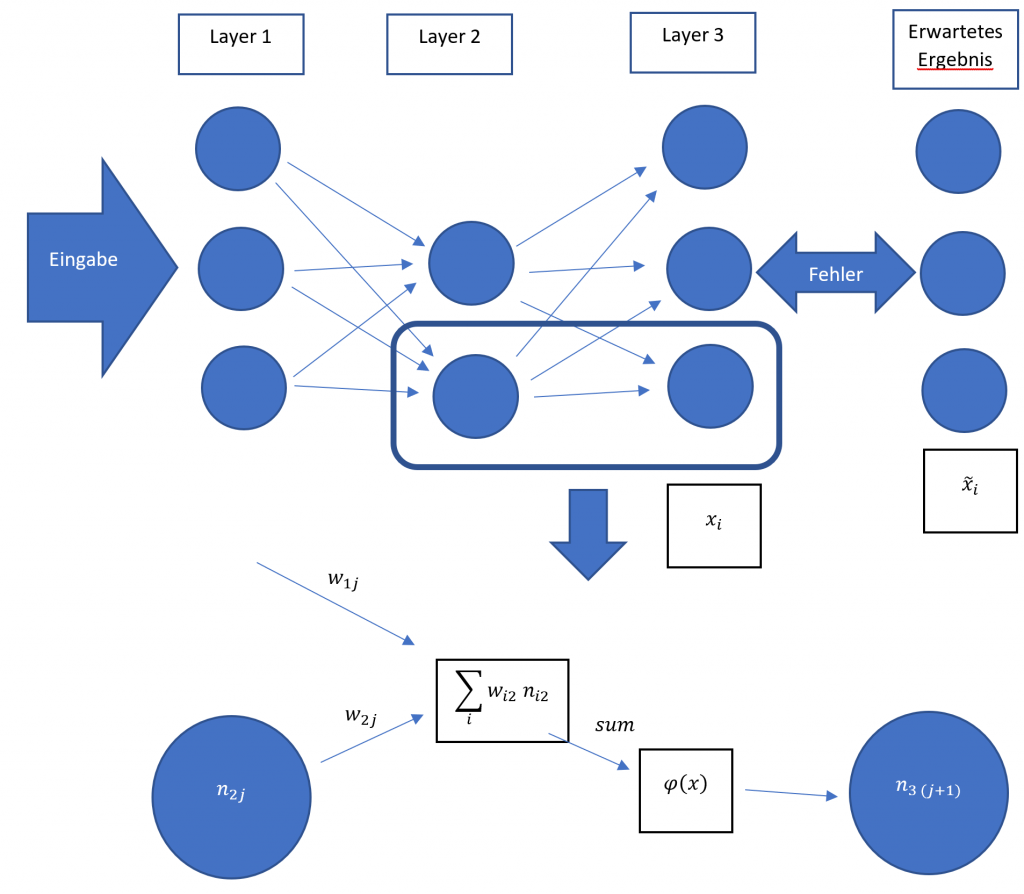
Es sei ein gewöhnliches deep neural network ohne Rekursionen mit N Layern gegeben. Die Gewichte sind mit wij bezeichnet wobei j<=N und i kleiner gleich der Anzahl der in dem jeweiligen Layer befindlichen Nodes ist. Speist man eine Eingabe bei relativ willkürlich initialisierten Gewichten ein, ergibt sich eine Abweichung vom gewünschten Ergebniss. Um diese Abweichung zu charakterisieren kann man eine Fehlerfunktion benutzen z.B. die Summe der Quadratischenfehler aus den Ausgangsnodes
E :=∑Outputnodesxi-x~i2
Nun möchten wir die Änderungsrate des Fehlers E in abhängigkeit zu jedem Gewicht w kennen also die Ableitung ∂E∂wij um zu wissen in welche Richtung w korrigiert werden muss um einen geringeren Fehler zu erhalten. Nach der Kettenregel gilt also

als φx verwenden wir eine sigmoide Funktion, die monoton steigend ist, durch die Grenzwerte 0 und 1 nach oben und unten beschränkt ist und möglichst einfach stetig differenzierbar ist.
φx=11+e-ax mit a∈R+
Dem entsprechend gilt für die Ableitung(Substitution und Partialbruchzerlegung):
∂xj∂ sum=∂φ∂xx=sum=ae-ax1+e-ax2x=sum=a1+e-ax-a1+e-ax2x=sum=a1+e-ax1-a1+e-axx=sum=φx1-φxx=sum=φsum1-φsum
∂ sum∂ wij=nij
∂E∂xj=∂∂xj∑Outputnodesxi-x~i2=2xj-x~j für Ausgabe-Nodes
Es ergibt sich eine Rekursive Definition. Für Ausgabe-Nodes gilt:
∂E∂wij=2 nij φsum1-φsumxj-x~j
für Hidden-Nodes
∂E∂wij=2 nij φsum1-φsum∑jϑj+1wi(j+1)
Bzw.
ϑj:= φsum1-φsumxj-x~j wenn j ein output Node ist φsum1-φsum∑jϑj+1wi(j+1) wenn j ein hidden Node ist
∂E∂wij=2nijϑj
Der Fehler soll iterativ minimiert werden also wird ∆wij zu
∆wij=-C'∂E∂wij=-C nijϑj
Gewählt wobei C :=C(t) mit der Iterationszahl t eine von der Iteration abhängige Lernrate beschreibt, die im simpelsten fall als konstant definiert wird. In einem Iterationsschritt berechnen sich die neuen Gewichte wie folgt:
wijnew= wijold+ ∆wij
Pro Trainingssample kann ein oder mehrmals iteriert werden. Um noch bessere Ergebnisse zu erzielen macht man ∆wij(t) von der vorhergehenden Iteration ∆wij(t-1) abhängig und führt z.B. einen Gewichtungsfaktor G ein, der von 0 bis 100 festlegt wie groß der Einfluss der Gewichtsänderung der vorhergehenden Iteration sein soll:
∆wij(t)=-Ct1-Gnijϑj+G ∆wij(t-1)
Dies sorgt anschaulich für eine endliche Beschleunigungsrate durch quadratische Effekte und hilft nicht multi-dimensionalen Nebenminima festzustecken.
Für weitere Optimierungen kann man je nach Anwendung für verschiedene Layer unterschiedliche Aktivierungsfunktionen verwenden die ReLu Funktion fx=max(0,x), die auf Grund der für Backpropagation notwendigen Differenzierbarkeit mit fx=ln(1+ex) approximiert ist z.B. auch oft nützlich. Neuere Ansätze benutzen auch eine wachsende Anzahl an Nodes um die Lerngeschwindigkeit bei hochkomplexen Netzen um Größenordnungen zu steigern. Netze solcher Art sind allerdings nur ein kleiner Baustein um größere künstlich „denkende“ Systeme mit rekursiven Pipelines oder gar eine hohe neuronale Programmiersprache aufzubauen. Es gilt also noch viel zu entdecken und zu experimentieren. Interessant ist vor allem auch, wie man ein fertig trainiertes System schaltungstechnisch in integrierte Hardware umsetzt ohne dabei platzraubende und kostenintensive elektrische Kapazitäten einsetzen zu müssen.